Comprised of a set of compiler directives, OpenACC was created to accelerate code using the many streaming multiprocessors (SM) present on a GPU. Similar to how OpenMP is used for accelerating code on multicore CPUs, OpenACC can accelerate code on GPUs. But OpenACC offers more, as it is compatible with multiple architectures and devices, including multicore x86 CPUs and NVIDIA GPUs.
Here we will examine some fundamentals of OpenACC by accelerating a small program consisting of iterations of simple matrix multiplication. Along the way, we will see how to use the NVIDIA Visual Profiler to identify parts of the code which call OpenACC compiler directives. Graphical timelines displayed by the NVIDIA Visual Profiler visually indicate where greater speedups can be achieved. For example, applications which perform excessive host to device data transfer (and vice versa), can be significantly improved by eliminating excess data transfer.
Industry Support for OpenACC
OpenACC is the result of a collaboration between PGI, Cray, and CAPS. It is an open specification which sets out compiler directives (sometimes called pragmas). The major compilers supporting OpenACC at inception came from PGI, Cray, and CAPS. The OpenACC Toolkit (which includes the PGI compilers) is available for download from NVIDIA
The free and open source GNU GCC compiler supports OpenACC. This support may trail the commercial implemenations.
Introduction to Accelerating Code with OpenACC
 OpenACC facilitates the process of accelerating existing applications by requiring changes only to compute-intense sections of code, such as nested loops. A nested loop might go through many serial iterations on a CPU. By adding OpenACC directives, which look like specially-formatted comments, the loop can run in parallel to save significant amounts of runtime. Because OpenACC requires only the addition of compiler directives, usually along with small amounts of re-writing of code, it does not require extensive re-factoring of code. For many code bases, a few dozen effectively-placed compiler directives can achieve significant speedup (though it should be mentioned that most existing applications will likely require some amount of modification before they can be accelerated to near-maximum performance).
OpenACC facilitates the process of accelerating existing applications by requiring changes only to compute-intense sections of code, such as nested loops. A nested loop might go through many serial iterations on a CPU. By adding OpenACC directives, which look like specially-formatted comments, the loop can run in parallel to save significant amounts of runtime. Because OpenACC requires only the addition of compiler directives, usually along with small amounts of re-writing of code, it does not require extensive re-factoring of code. For many code bases, a few dozen effectively-placed compiler directives can achieve significant speedup (though it should be mentioned that most existing applications will likely require some amount of modification before they can be accelerated to near-maximum performance).
OpenACC is relatively new to the set of frameworks, software development kits, and programming interfaces available for accelerating code on GPUs. In June 2013, the 2.0 stable release of OpenACC was introduced. OpenACC 3.0 is current as of November 2019. The 1.0 stable release of OpenACC was first made available in November, 2011.
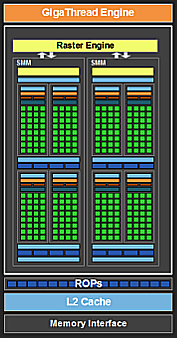
By reading OpenACC directives, the compiler assembles CUDA kernels from each section of compute-intense code. Each CUDA kernel is a portion of code that will be sent to the many GPU Streaming Multiprocessor processing elements for parallel execution (see Figure 1).
The Compute Unified Device Architecture (CUDA) is an application programming interface (API), which was developed by NVIDIA for the C and Fortran languages. CUDA allows for parallelization of computationally-demanding applications. Those looking to use OpenACC do not need to know CUDA, but those looking for maximum performance usually need to use some direct CUDA calls. This is accomplished either by the programmer writing tasks as CUDA kernels, or by calling a CUDA ‘drop-in’ library. With these libraries, a developer invokes accelerated routines without having to write any CUDA kernels. Such CUDA ‘drop-in’ libraries include CUBLAS, CUFFT, CURAND, CUSPARSE, NPP, among others. The libraries mentioned here by name are included in the freely available CUDA toolkit.
While OpenACC makes it easier for scientists and engineers to accelerate large and widely-used code bases, it is sometimes only the first step. With CUDA, a more extensive process of code refactoring and acceleration can be undertaken. Greater speedups can be achieved using CUDA. OpenACC is therefore a relatively easy first step toward GPU acceleration. The second (optional), and more challenging step requires code refactoring with CUDA.
OpenACC Parallelization Reports
There are several tools available for reporting information on the parallel execution of an OpenACC application. Some of these tools run within the terminal and are text-based. The text reports can be generated by setting particular environment variables (more on this below), or by invoking compiler options when compiling at the command line. Text reports will provide detail on which portions of the code can be accelerated with kernels.
The NVIDIA Visual Profiler, has a graphical interface which displays a timeline detailing when data transfers occur between the host and device. Kernel launches and runtimes are indicated with a colored horizontal bar. The graphical timeline and text reports in the terminal together provide important information which could indicate sections of code that are reducing performance. By locating inefficiencies in data transfers, for example, the runtime can be reduced by restructuring parallel regions. The example below illustrates a timeline report showing excessive data transfers between the system and the GPU (the host and the device).
Applying OpenACC to Accelerate Matrix Operations
Start with a Serial Code
To illustrate OpenACC usage, we will examine an application which performs common matrix operations. To begin, look at the serial version of the code (without OpenACC compiler directives) in Figure 2:
[sourcecode language=”C”]
#include "stdio.h"
#include "stdlib.h"
#include "omp.h"
#include "math.h"
void fillMatrix(int size, float **restrict A) {
for (int i = 0; i < size; ++i) {
for (int j = 0; j < size; ++j) {
A[i][j] = ((float)i);
}
}
}
float** MatrixMult(int size, float **restrict A, float **restrict B,
float **restrict C) {
for (int i = 0; i < size; ++i) {
for (int j = 0; j < size; ++j) {
float tmp = 0.;
for (int k = 0; k < size; ++k) {
tmp += A[i][k] * B[k][j];
}
C[i][j] = tmp;
}
}
return C;
}
float** MakeMatrix(int size, float **restrict arr) {
int i;
arr = (float **)malloc( sizeof(float *) * size);
arr[0] = (float *)malloc( sizeof(float) * size * size);
for (i=1; i<size; i++){
arr[i] = (float *)(arr[i-1] + size);
}
return arr;
}
void showMatrix(int size, float **restrict arr) {
int i, j;
for (i=0; i<size; i++){
for (j=0; j<size; j++){
printf("arr[%d][%d]=%f \n",i,j,arr[i][j]);
}
}
}
void copyMatrix(float **restrict A, float **restrict B, int size){
for (int i=0; i<size; ++i){
for (int j=0; j<size; ++j){
A[i][j] = B[i][j];
}
}
}
int main (int argc, char **argv) {
int i, j, k;
float **A, **B, **C;
if (argc != 3) {
fprintf(stderr,"Use: %s size nIter\n", argv[0]);
return -1;
}
int size = atoi(argv[1]);
int nIter = atoi(argv[2]);
if (nIter <= 0) {
fprintf(stderr,"%s: Invalid nIter (%d)\n", argv[0],nIter);
return -1;
}
A = (float**)MakeMatrix(size, A);
fillMatrix(size, A);
B = (float**)MakeMatrix(size, B);
fillMatrix(size, B);
C = (float**)MakeMatrix(size, C);
float startTime_tot = omp_get_wtime();
for (int i=0; i<nIter; i++) {
float startTime_iter = omp_get_wtime();
C = MatrixMult(size, A, B, C);
if (i%2==1) {
//multiply A by B and assign back to A on even iterations
copyMatrix(A, C, size);
}
else {
//multiply A by B and assign back to B on odd iterations
copyMatrix(B, C, size);
}
float endTime_iter = omp_get_wtime();
}
float endTime_tot = omp_get_wtime();
printf("%s total runtime %8.5g\n", argv[0], (endTime_tot-startTime_tot));
free(A); free(B); free(C);
return 0;
}
[/sourcecode]
Figure 2 Be sure to include the stdio.h and stdlib.h header files. Without these includes, you may encounter segmentation faults during dynamic memory allocation for 2D arrays.
If the program is run in the NVIDIA Profiler without any OpenACC directive, a console output will not include a timeline. Bear in mind that the runtime displayed in the console includes runtime overhead from the profiler itself. To get a more accurate measurement of runtime, run without the profiler at the command line. To compile the serial executable with the PGI compiler, run:
pgcc -fast -o ./matrix_ex_float ./matrix_ex_float.c
The serial runtime, for five iterations with 1000x1000 matrices, is 7.57 seconds. Using larger 3000x3000 matrices, with five iterations increases the serial runtime to 265.7 seconds.
Parallelizing Matrix Multiplication
The procedure-calling iterative loop within main() cannot, in this case, be parallelized because the value of matrix A depends on a series of sequence-dependent multiplications. This is the case with all sequence-dependent evolution of data, such as with time stepped iterations in molecular dynamics (MD). In an obvious sense, loops performing time evolution cannot be run in parallel, because the causality between discrete time steps would be lost. Another way of stating this is that loops with backward dependencies cannot be made parallel.
With the application presented here, the correct matrix product is dependent on the matrices being multiplied together in the correct order, since matrix multiplication does not commute, in general. If the loop was run in parallel, the outcome would be unpredictable, and very likely not what the programmer intended. For example, the correct output for our application, after three iterations, takes on the form AxBxAxBxB. This accounts for the iterative reassignments of A and B to intermediate forms of the product matrix, C. After four iterations, the sequence becomes AxBxAxBxBxAxBxB. The main point: if this loop were to run in parallel, this sequence would very likely be disrupted into some other sequence, through the uncontrolled process of which threads, representing loop iterations, execute before others on the GPU.
[sourcecode language=”C”]
for (int i=0; i<nIter; i++) {
float startTime_iter = omp_get_wtime();
C = MatrixMult(size, A, B, C);
if (i%2==1) {
//multiply A by B and assign back to A on even iterations
copyMatrix(A, C, size);
}
else {
//multiply A by B and assign back to B on odd iterations
copyMatrix(B, C, size);
}
float endTime_iter = omp_get_wtime();
}
[/sourcecode]
We’ve established that the loop in main() is non-parallelizable, having an implicit dependence on the order of execution of loop iterations. To achieve a speedup, one must examine the routine within the loop: MatrixMult()
[sourcecode language=”C”]
float** MatrixMult(int size, float **restrict A, float **restrict B,
float **restrict C) {
#pragma acc kernels pcopyin(A[0:size][0:size],B[0:size][0:size]) \
pcopyout(C[0:size][0:size])
{
float tmp;
for (int i=0; i<size; ++i) {
for (int j=0; j<size; ++j) {
tmp = 0.;
for (int k=0; k<size; ++k) {
tmp += A[i][k] * B[k][j];
}
C[i][j] = tmp;
}
}
}
return C;
}
[/sourcecode]
Here, a kernels OpenACC directive has been placed around all three for loops. Three loops happens to be the maximum number of nested loops that can be parallelized within a single nested structure. Note the syntax for an OpenACC compiler directive in C takes on the following form:
#pragma acc kernels [clauses]
In the code above, the kernels directive tells the compiler that it should try to convert this section of code into a CUDA kernel for parallel execution on the device. Instead of describing a long list of OpenACC directives here, an abbreviated list of commonly used directives appears below in Table 1 (see the references for complete API documentation):
| Commonly used OpenACC directives | |
|---|---|
#pragma acc parallel | Start parallel execution on the device. The compiler will generate parallel code whether the result is correct or not. |
#pragma acc kernels | Hint to the compiler that kernels may be generated for the defined region. The compiler may generate parallel code for the region if it determines that the region can be accelerated safely. Otherwise, it will output warnings and compile the region to run in serial. |
#pragma acc data | Define contiguous data to be allocated on the device; establish a data region minimizing excessive data transfer to/from GPU |
#pragma acc loop | Define the type of parallelism to apply to the proceeding loop |
#pragma acc region | Define a parallel region where the compiler will search for code segments to accelerate. The compiler will attempt to automatically parallelize whatever it can, and report during compilation exactly what portions of the parallel region have been accelerated. |
Table 1 OpenACC Compiler Directives
Along with directives, there can be modifying clauses. In the example above, we are using the kernels directive with the pcopyin(list) and pcopyout(list) clauses. These are abbreviations for present_or_copyin(list), and present_or_copyout(list).
pcopy(list)tells the compiler to copy the data to the device, but only if data is not already present. Upon exiting from the parallel region, any data which is present will be copied to the host.pcopyin(list)tells the compiler to copy to the device if the data is not already there.pcopyout(list)directs the compiler to copy the data if it is on the device, else the data is allocated to the device memory and then copied to the host. The variables, and arrays inlistare those which will be copied.present_or_copy(list)clauses avoid the reduced performance of excessive data copies, since the data needed may already be present.
After adding the kernels directive to MatrixMult(), compile and run the executable in the profiler. To compile a GPU-accelerated OpenACC executable with PGI, run:
pgcc -fast -acc -ta=nvidia -Minfo -o ./matrix_ex_float ./matrix_ex_float.c
The -Minfo flag is used to enable informational messages from the compiler. These messages are crucial for determining whether the compiler is able to apply the directives successfully, or whether there is some problem which could possibly be solved. For an example of a compiler message reporting a warning, see the section ‘Using a Linearized Array Instead of a 2D Array’ in the next OpenACC blog, entitled ‘More Tips on OpenACC Code Acceleration‘.
To run the executable in the NVIDIA Visual Profiler, run:
nvvp ./matrix_ex 1000 5
During execution, the 1000x1000 matrices – A and B – are created and multiplied together into a product. The command line argument 1000 specifies the dimensions of the square matrix and the argument 5 sets the number of iterations for the loop to run through. The NVIDIA Visual Profiler will display the timeline below:
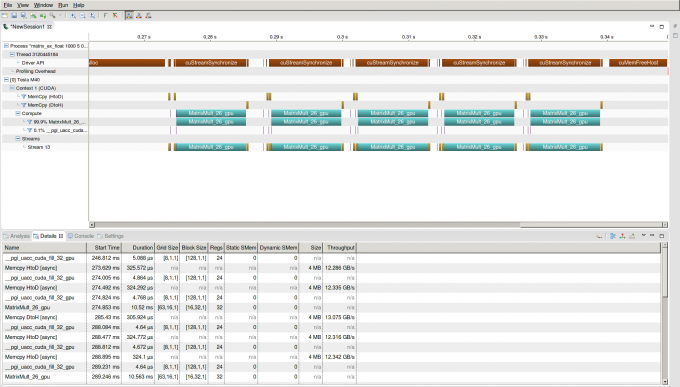
Note that there are two Host to Device transfers of matrices A and B at the start of every iteration. Data transfers to the device, occurring after the first transfer, are excessive. In other words, every data copy after the first one is wasted time and lost performance.
Using the OpenACC data Directive to Eliminate Excess Data Transfer
Because the parallel region consists of only the two loops in the MatrixMult() routine, every time this routine is called entire copies of matrices A & B are passed to the device. Since the data only needs to be sent before the first iteration, it would make sense to expand the data region to encompass every call to MatrixMult(). The boundary of the data region must be pushed out to encompass the loop in main(). By placing a data directive just outside of this loop, as shown in Figure 4, the unnecessary copying of A and B to the device after the first iteration is eliminated:
[sourcecode language=”C”]
#pragma acc data pcopyin(A[0:size][0:size],B[0:size][0:size],C[0:size][0:size]) \
pcopyout(C[0:size][0:size])
{
float startTime_tot = omp_get_wtime();
for (int i=0; i<nIter; i++) {
float startTime_iter = omp_get_wtime();
C = MatrixMult(size, A, B, C);
if (i%2==1) {
//multiply A by B and assign back to A on even iterations
copyMatrix(A, C, size);
}
else {
//multiply A by B and assign back to B on odd iterations
copyMatrix(B, C, size);
}
float endTime_iter = omp_get_wtime();
}
float endTime_tot = omp_get_wtime();
}
[/sourcecode]
Figure 4 A data region is established around the for loop in main()
After recompiling and re-running the executable in NVIDIA’s Visual Profiler nvvp, the timeline in Figure 5 shows that the unnecessary transfers are now gone:
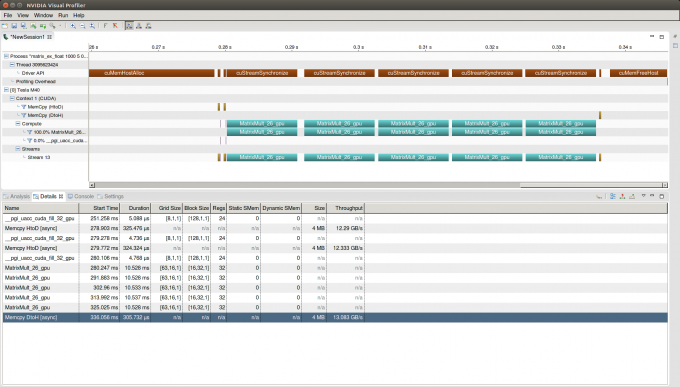
Now matrices A and B are copied to the device only once. Matrix C, the result, is copied to the Host at the end of the kernel region in MatrixMult() on every iteration. As shown in the table below, the runtime improvement is small but significant (1.9s vs. 1.5s). This reflects a 19.5% decrease in runtime; a speedup of 1.24.
| Runtimes for Various OpenACC Methods (in seconds) | ||
|---|---|---|
| OpenACC method | Matrix size 1000×1000 | Matrix size 3000×3000 |
| no acceleration | 7.569 | 265.69 |
#pragma acc kernels in MatrixMult() | 0.3540 | 1.917 |
#pragma acc kernels in MatrixMult() and #pragma acc data in main() | 0.0539 | 1.543 |
Table 2 Runtimes for five iterations of matrix multiplication (C=AxB).
As data sizes increase, the amount of work grows and the benefits of parallelization become incredibly clear. For the larger 3000x3000 matrices, a speedup factor of 172 is realized when both kernels and data directives are used.
Comparing Runtimes of OpenACC and OpenMP
Because OpenMP is also used as a method for parallelization of applications, it is useful to compare the two. To compare OpenACC with OpenMP, an OpenMP directive is added to the MatrixMult() routine:
[sourcecode language=”C”]
void MatrixMult(int size, float **restrict A, float **restrict B,
float **restrict C) {
#pragma acc kernels pcopyin(A[0:size][0:size],B[0:size][0:size]) \
pcopyout(C[0:size][0:size])
#pragma omp parallel for default(none) shared(A,B,C,size)
for (int i=0; i<size; ++i) {
for (int j=0; j<size; ++j) {
float tmp = 0.;
for (int k=0; k<size; ++k) {
tmp += A[i][k] * B[k][j];
}
C[i][j] = tmp;
}
}
}
[/sourcecode]
To compile the code with OpenMP parallelization, run:
pgcc -fast -mp ./matrix_ex_float.c -o ./matrix_ex_float_omp
The results were gathered on a Microway NumberSmasher server with dual 12-core Intel Xeon E5-2690v3 CPUs running at 2.6GHz. Runtimes were gathered when executing on 6, 12, and 24 of the CPU cores. This is achieved by setting the environment variable OMP_NUM_THREADS to 6, 12, and 24 respectively.
| Number of Threads | Runtime (in seconds) |
|---|---|
| 6 | 37.758 |
| 12 | 18.886 |
| 24 | 10.348 |
Table 3 Runtimes achieved with OpenMP using 3000x3000 matrices and 5 iterations
It is clear that OpenMP is able to provide parallelization and good speedups (nearly linear). However, the GPU accelerators are able to provide more compute power than the CPUs. The results in Table 4 demonstrate that OpenMP and OpenACC both substancially increase performance. By utilizing a single NVIDIA Tesla M40 GPU, OpenACC is able to run 6.71 faster than OpenMP.
| Speedups Over Serial Runtime | |||
|---|---|---|---|
| serial | OpenMP speedup | OpenACC speedup | |
| 1 | 25.67x | 172x | |
Table 4 Relative Speedups of OpenACC and OpenMP for 3000x3000 matrices.
OpenACC Bears Similarity to OpenMP
As previously mentioned, OpenACC shares some commonality with OpenMP. Both are open standards, consisting of compiler directives for accelerating applications. Open Multi-Processing (OpenMP) was created for accelerating applications on multi-core CPUs, while OpenACC was primarily created for accelerating applications on GPUs (although OpenACC can also be used to accelerate code on other target devices, such as multi-core CPUs). Looking ahead, there is a growing consensus that the roles of OpenMP and OpenACC will become more and more alike.
OpenACC Acceleration for Specific GPU Devices
GPU Hardware Specifics
When a system has multiple GPU accelerators, a specific GPU can be selected either by using an OpenACC library procedure call, or by simply setting the environment variable CUDA_VISIBLE_DEVICES in the shell. For example, this would select GPUs #0 and #5:
export CUDA_VISIBLE_DEVICES=0,5
On Microway’s GPU Test Drive Cluster, some of the Compute Nodes have a mix of GPUs, including two Tesla M40 GPUs labelled as devices 0 and 5. To see what devices are available on your machine, run the command deviceQuery, (which is included with the CUDA Toolkit). pgaccelinfo, which comes with the OpenACC Toolkit, reports similar information.
When an accelerated application is running, you can view the resource allocation on the device by executing the nvidia-smi utility. Memory usage and GPU usage, listed by application, are reported for all GPU devices in the system.
Gang, Worker, and Vector Clauses
Although CUDA and OpenACC both use similar ideas, their terminology differs slightly. In CUDA, parallel execution is organized into grids, blocks (threadBlocks), and threads. In OpenACC, a gang is like a CUDA threadBlock, which executes on a processing element (PE). On a GPU device, the processing element (PE) is the streaming multiprocessor (SM). A number of OpenACC gangs maps across numerous PEs (CUDA blocks).
An OpenACC worker is a group of vectors. The worker dimension extends across the height of a gang (threadBlock). Each vector is a CUDA thread. The dimension of vector is across the width of the threadBlock. Each worker consists of vector number of threads. Therefore, a worker corresponds to one CUDA warp only if vector takes on the value of 32; a worker does not have to correspond to a warp. For example, a worker can correspond to two warps if vector is 64, for example. The significance of a warp is that all threads in a warp run concurrently.
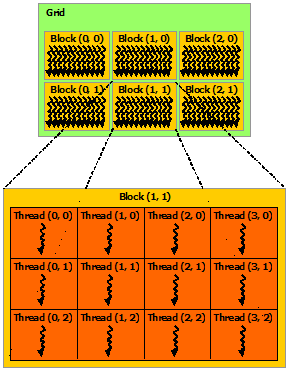
Figure 6 illustrates a threadBlock, represented as part of a 2D grid containing multiple threadBlocks. In OpenACC, the grid consists of a number of gangs, which can extend into one or two dimensions. As depicted in Figure 7, the gangs extend into one dimension. It is possible, however, to arrange gangs into a two dimensional grid. Each gang, or threadBlock, in both figures 6 and 7 is comprised of a 2D block of threads. The number of vectors, workers, and gangs can be finely tuned for a parallel loop.
Sometimes it is faster to have some kernels execute more than once on a block, instead of having each kernel execute only once per block. Discovering the optimal amount of kernel re-execution can require some trial and error. In OpenACC, this would correspond to a case where the number of gangs is less than a loop layer which is run in parallel across gangs and which has more iterations than gangs available.
In CUDA, threads execute in groups of 32 at a time. Groups of 32 threads, as mentioned, are called warps, and execute concurrently. In Figure 8, the block width is set to 32 threads. This makes more threads execute concurrently, so the program runs faster.
[expand title=”(click to expand) Additional runtime output, with kernel runtimes, grid size, and block size”]
Note: the kernel reports can only be generated by compiling with the time target, as shown below (read more about this in our next blog post). To compile with kernel reports, run:
pgcc -fast -acc -ta=nvidia,time -Minfo -o ./matrix_ex_float ./matrix_ex_float.c
Once the executable is compiled with the nvidia and time arguments, a kernel report will be generated during execution:
[john@node6 openacc_ex]$ ./matrix_ex_float 3000 5 ./matrix_ex_float total runtime 1.3838 Accelerator Kernel Timing data /home/john/MD_openmp/./matrix_ex_float.c MatrixMult NVIDIA devicenum=0 time(us): 1,344,646 19: compute region reached 5 times 26: kernel launched 5 times grid: [100x100] block: [32x32] device time(us): total=1,344,646 max=269,096 min=268,685 avg=268,929 elapsed time(us): total=1,344,846 max=269,144 min=268,705 avg=268,969 19: data region reached 5 times 35: data region reached 5 times /home/john/MD_openmp/./matrix_ex_float.c main NVIDIA devicenum=0 time(us): 8,630 96: data region reached 1 time 31: data copyin transfers: 6 device time(us): total=5,842 max=1,355 min=204 avg=973 31: kernel launched 3 times grid: [24] block: [128] device time(us): total=19 max=7 min=6 avg=6 elapsed time(us): total=509 max=432 min=34 avg=169 128: data region reached 1 time 128: data copyout transfers: 3 device time(us): total=2,769 max=1,280 min=210 avg=923
[/expand]
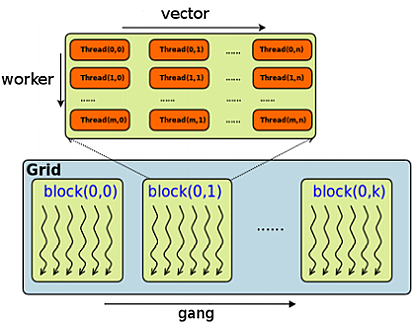
worker, and horizontal dimension vector. The grid consists of gang threadBlocks.[sourcecode language=”C”]
float** MatrixMult(int size, int nr, int nc, float **restrict A, float **restrict B,
float **restrict C) {
#pragma acc kernels loop pcopyin(A[0:size][0:size],B[0:size][0:size]) \
pcopyout(C[0:size][0:size]) gang(100), vector(32)
for (int i = 0; i < size; ++i) {
#pragma acc loop gang(100), vector(32)
for (int j = 0; j < size; ++j) {
float tmp = 0.;
#pragma acc loop reduction(+:tmp)
for (int k = 0; k < size; ++k) {
tmp += A[i][k] * B[k][j];
}
C[i][j] = tmp;
}
}
return C;
}
[/sourcecode]
Figure 8 OpenACC code with gang and vector clauses. The fully accelerated OpenACC version of the C source code can be downloaded here.
The directive clause gang(100), vector(32), on the j loop, sets the block width to 32 threads (warp size), which makes parallel execution faster. Integer multiples of a warp size will also realize greater concurrency, but not usually beyond a width of 64. The same clause sets the grid width to 100. The directive clause on the outer i loop, gang(100), vector(32), sets the grid height to 100, and block height to 32. The block height specifies that the loop iterations are processed in SIMT groups of 32.
By adding the gang and vector clauses, as shown in Figure 8, the runtime is reduced to 1.3838 sec (a speedup of 1.12x over the best runtime in Table 2).
Targeting GPU Architectures with the Compiler
OpenACC is flexible in its support for GPU, which means support for a variety of GPU types and capabilities. The target options in the table below illustrate how different compute capabilities, GPU architectures, and CUDA versions can be targeted.
| compute capability | GPU architecture | CUDA version | CPU |
|---|---|---|---|
| -ta=nvidia[,cc10|cc11|cc12|cc13|cc20] -ta=tesla:cc35, -ta=nvidia,cc35 | -ta=tesla, -ta=nvidia | -ta=cuda7.5, -ta=tesla:cuda6.0 | -ta=multicore |
Table 5 Various GPU target architecture options for the OpenACC compiler
OpenACC for Fortran
Although we have focused here on using OpenACC in the C programming language, there is robust OpenACC support for the Fortran language. The syntax for compiler directives is only slightly different. In the C language, with dynamic memory allocation and pointers, pointers must be restricted inside of parallel regions. This means that pointers, if not declared as restricted in main(), or subsequently cast as restricted in main(), must be cast as restricted when passed as input arguments to routines containing a parallel region. Fortran does not use pointers and handles memory differently, with less user control. Pointer-related considerations therefore do not arise with Fortran.
Summary
OpenACC is a relatively recent open standard for acceleration directives which is supported by several compilers, including, perhaps most notably, the PGI compilers.
Accelerating code with OpenACC is a fairly quick route to speedups on the GPU, without needing to write CUDA kernels in C or Fortran, thereby removing the need to refactor potentially numerous regions of compute-intense portions of a large software application. By making an easy path to acceleration accessible, OpenACC adds tremendous value to the CUDA API. OpenACC is a relatively new development API for acceleration, with the stable 2.0 release appearing in June 2013.
If you have an application and would like to get started with accelerating it with OpenACC or CUDA, you may want to try a free test drive on Microway’s GPU Test Cluster. On our GPU servers, you can test your applications on the Tesla K40, K80, or the new M40 GPU specialized for Deep Learning applications. We offer a wide range of GPU solutions, including:
- Acoustically-insulated Quadro GPU WhisperStations, which are quiet desktop supercomputers
- Microway WhisperStation for Deep Learning
- GPU-accelerated server systems and HPC Clusters