In my previous post, I presented a brief introduction to the CUB library of CUDA primitives written by Duane Merrill of NVIDIA. CUB provides a set of highly-configurable software components, which include warp- and block-level kernel components as well as device-wide primitives. This time around, we will actually look at performance figures for codes that utilize CUB primitives. We will also briefly compare the CUB-based codes to programs that use the analogous Thrust routines, both from a performance and programmability perspective. These comparisons utilize the CUB v1.3.1 and Thrust v1.7.0 releases and CUDA 6.0.
Before we proceed, I need to issue one disclaimer: the examples below were written after a limited amount of experimentation with the CUB library, and they do not necessarily represent the most optimized implementations. However, these examples do illustrate the flexibility of the API and they give an idea of the kind of performance that can be achieved using CUB with only modest programming effort.
Computing Euclidean vector norms – transformations and reductions
To begin with, let’s consider a variant of the reduction routine, which reads in a data array and computes the sum of the squares of the array elements. If we interpret the array as a vector, then the square root of the result of the reduction gives the Euclidean norm, or L2 norm, of the vector.
A kernel implementation that uses CUB’s block-level primitives is shown below:
template<typename T, int BLOCK_THREADS, int ITEMS_PER_THREAD,
BlockReduceAlgorithm ALGORITHM, typename U>
__global__ void TransformSumKernel(T* sum, T* input, U unaryOp)
{
typedef BlockReduce<T, BLOCK_THREADS, ALGORITHM> BlockReduceT;
__shared__ typename BlockReduceT::TempStorage temp_storage;
T data[ITEMS_PER_THREAD];
LoadDirectBlockedVectorized(threadIdx.x
input+blockIdx.x*BLOCK_THREADS*ITEMS_PER_THREAD,
data);
for(int item=0; item<ITEMS_PER_THREAD; ++item)
data[item] = unaryOp(data[item]);
T block_sum = BlockReduceT(temp_storage).Sum(data);
if(threadIdx.x==0) atomicAdd(sum,block_sum);
return
}
In this example, each thread block processes a tile of BLOCK_THREADS*ITEMS_PER_THREAD input elements, and for simplicity the size of the input array is assumed to be a multiple of the tile size. As its name suggests, the function LoadDirectBlockedVectorized uses vectorized loads to increase memory bandwidth utilization. (We could also have used the higher-level BlockLoad class to perform the global-memory loads. The BlockLoad class is templated on the load algorithm, making it trivial to switch between vectorized loads and other approaches.) Global memory loads are coalesced provided that ITEMS_PER_THREAD does not exceed the maximum allowed vector-load width (for example, four ints or floats). unaryOp is a unary C++ function object. In order to compute the sum of the squares of the elements of the input array, we choose unaryOp to be an instance of the Square<T> class, which is defined as follows:
template<typename T>
struct Square
{
__host__ __device__ __forceinline__
T operator()(const T& a) const {
return a*a;
}
};
CUB Block-level primitives and fancy iterators
CUB’s iterator classes facilitate more elegant and generic kernel implementations. The library contains a number of iterator classes, including iterators that implement textures and iterators that support various cache modifiers for memory accesses. However, for the moment, let’s just consider the TransformInputIterator class, which has the following declaration:
template < typename ValueType, typename ConversionOp, typename InputIterator,
typename Offset=ptr_diff >
class TransformInputIterator;
In this declaration, InputIterator is another iterator type, which could simply be a pointer to a native device type; ConversionOp is a unitary operator class, such as the Square class defined above; and ValueType is the input value type. The precise meaning of these template arguments should become clear in the discussion below. Utilizing iterators, we can compute the Euclidean norm squared using the following reduction-kernel template:
template<typename T, int BLOCK_THREADS, int ITEMS_PER_THREAD,
BlockReduceAlgorithm ALGORITHM, typename I>
__global__ void SumKernel(T* sum, I input_iter)
{
typedef BlockReduct<T BLOCK_THREADS, ALGORITHM> BlockReduceT;
__shared__ typename lockReduceT::TempStorage temp_storage;
T data[ITEMS_PER_THREAD];
LoadDirectStriped<BLOCK_THREADS>(threadIdx.x
input_iter + blockIdx.x*blockDim.xTEMS_PER_THREAD,
data);
T block_sum = BlockReduceT(temp_storage).Sum(data);
if(threadIdx.x == 0) atomicAdd(sum,block_sum)
return;
}
where input_iter is an instance of the TransformInputIterator class:
TransformInputIterator<T, Square<T>, T*> input_iter(input, Square<T>());
At present, CUB only supports vectorized loads for native device-type pointers, and the above kernel template uses the LoadDirectStriped<BLOCK_THREADS> routine to load data from global memory. Each thread loads ITEMS_PER_THREAD array elements separated by stride BLOCK_THREADS from global memory. BLOCK_THREADS is, of course, a multiple of the warp size, and data loads are coalesced.
Device-wide primitives
CUB contains a range of device-level primitives, including a device-wide reduction optimized for different architectures. Therefore, the only reason for implementing custom kernels for this particular calculation is that they might provide some performance advantage. The calculation can be implemented with CUB’s device-level API by using the input iterator defined above and calling
DeviceReduce::Sum(temp_storage,temp_storage_bytes,input_iter,output,num_elements);
The squared norm is then returned in the variable output. The same calculation can be performed using the Thrust library by calling
thrust::transform_reduce(d_in.begin(), d_in.end(), Square(), static_cast(0), thrust::plus())
in the client application.
CUB Performance
Fig. 1 shows performance data for codes that use the reduction kernels defined above, together with performance results for code using the DeviceReduce::Sum primitive. The corresponding performance figures for thrust::transform_reduce are also shown. These results were obtained on tests involving 32-bit floating-point data running on a Tesla K40c. Limited experimentation indicated that setting the thread-block size (BLOCK_THREADS) to 128 gave the best performance for both SumKernel and TransformSumKernel, and the block-wide reduction algorithm was set to BLOCK_REDUCE_RAKING_COMMUTATIVE_ONLY in both cases. The number of data items processed per thread (ITEMS_PER_THREAD) was set to 4 in runs involving TransformSumKernel, which uses vectorized loads. Choosing ITEMS_PER_THREAD=8, gave better performance in SumKernel. On all problem sizes, the CUB-based codes significantly outperform the code that utilizes the transform_reduce Thrust routine. We also see that the code that utilizes the DeviceReduce::Sum primitive is always competitive with code that utilizes our hand-tuned kernels, and, in fact, gives the best performance on all but the largest input arrays. This result is very encouraging since the use of CUB’s device-wide primitives in a client application requires very little programming effort, comparable to the effort required to utilize the corresponding Thrust primitives.
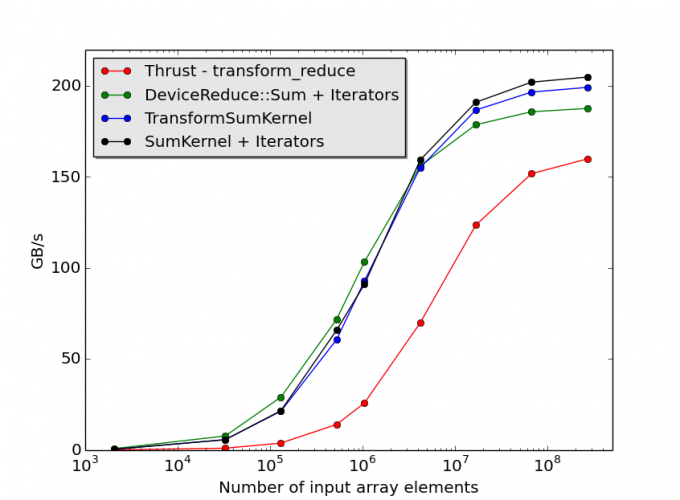
Fig. 1 – Performance measurements for the calculation of the square of the Euclidean norm of a float32 vector on a Tesla K40c
A second CUB example – Transformed prefix sum
Let’s consider the slightly more contrived example of the calculation of the inclusive prefix sum of the squares of the elements of an integer array. Given the input and output arrays int a_in[N] and int a_out[N], this calculation corresponds to the following serial C++ code:
a_out[0] = a_in[0]*a_in[0];
for(int i=1; i<N; ++i){
a_out[i] = a_in[i]*a_in[i] + a_out[i-1];
}
In analogy to the reduction example above, the calculation can also be implemented using CUB’s DeviceScan::InclusiveSum function together with the TransformInputIterator class. We tested the CUB-based approach and an implementation using Thrust on 32-bit integer data on a Tesla K40c. However, in our initial tests the CUB-based implementation showed lower-than-expected performance on large input arrays. These performance figures correspond to the green points in Fig. 2 below, where the input iterator passed to DeviceScan::InclusiveSum was of type TransformInputIterator<int, Square<int>, int*>. In fact, on the largest input arrays, better performance was obtained from the Thrust-based code (red points). Furthermore, we found that the code obtained by omitting the square operation and simply passing a pointer to the data in global memory (in this case, an int* pointer) to DeviceScan::InclusiveSum achieved approximately twice the performance on large problem sizes.
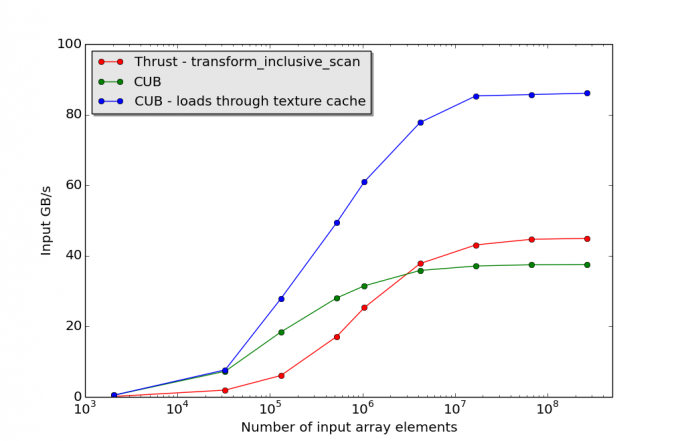
Fig. 2 – Performance of code to compute the inclusive prefix sum of the squared elements of an int32 array measured on a Tesla K40c
A quick look at the CUB source code revealed the reason for the disparity in performance. It turns out that on compute-capability 3.5 devices, DeviceScan::InclusiveSum is configured to load data through texture cache automatically – provided the input iterator is a pointer to a native device type. However, for more general iterator types, the use of texture cache has to be specified explicitly in the client application. Fortunately, this is easy to implement using the CacheModifiedInputIterator class defined in CUB. To utilize texture cache, input_iter, the iterator passed to the prefix-sum routine, should be defined as follows in the client code:
// loads using cached_iter go through texture cache on sm_35 devices CacheModifiedInputIterator<LOAD_LDG,int> cached_iter(d_in); // Use the following iterator to return the squares of the data elements // loaded from global memory using cached_iter TransformInputIterator<int,Square<int>, CacheModifiedInputIterator<LOAD_LDG,int> > input_iter(cached_iter, Square<int>());
The LOAD_LDG template argument specifies the use of texture cache on sm_35 hardware. The blue points in Fig. 2 correspond to performance figures obtained using the LOAD_LDG option, which, on large data sets, gives a 2x speedup over the code that does not utilize texture cache. CUB’s iterators support a number of other access modes, and although a comprehensive discussion of iterators is beyond the scope of this post, we encourage the reader to explore the iterator classes.
Summary
In this post, we have looked at variants of the reduction and prefix-sum algorithms that involve a transformation of the input data and how they might be implemented using the CUB library. In particular, we’ve considered implementations involving CUB’s device-level functions and iterator classes. These implementations compare favorably with code based on custom kernels and offer superior performance to the corresponding Thrust-based implementations. The examples also illustrate the flexibility and composability provided by CUB’s iterator classes.














